Table of Contents
Method Of Chaining On Level Ground
Before starting the chaining operation, two ranging rods should be fixed on the chain line, at the top stations.
The opposite ranging rod, should be fixed near the top of every chain length, during the ranging operation.
To chain the line, the leader moves forward by dragging the chain and by taking with him a ranging rod and ten arrows.
The follower stands at the starting station by holding the opposite end of the chain.
While the chain is completely elongated, the leader holds the ranging rod vertically at arm’s length.
The follower directs the leader to maneuver his rod to the left or right until the ranging rod is precisely in line.
Then the follower lays the zero end in the chain by touching the station peg. The leader stretches the chain by moving it up and down with both hands, and at last places it on the road .
He then inserts an arrow on the bottom at the end of the chain and marks with a cross (‘x’).
Again, the leader moves forward by dragging the chain with 9 arrows and therefore the ranging rod. To the end of the chain, he fixes another arrow as earlier.
As the leader moves there, the follower picks up the arrows which were inserted by the leader.
And during chaining, the surveyor or an assistant should conduct the ranging operation.
In this way, chaining is sustained . When all the arrows are inserted and therefore the leader has none left with him, the follower hands them over to the leader; this could be noted by the surveyor.
To measure the remaining fractional length, the leader should drag the chain beyond the station and also the follower should hold the zero end of the chain at the last arrow.
Then the odd links should be counted.
Method Of Chaining On Sloped Ground
Horizontal distances have required in surveying. So, in chaining toward a sloping ground, the horizontal distances between two stations are measured carefully by applying some convenient methods.
The following are the various methods that are generally employed:
1. Direct method or stepping method, and
2. Indirect method.
1. Direct Method
This method is applied when the slope of the surface of earth is extremely steep.
During this method, the sloping ground is split into a number of horizontal and vertical strips, like steps.
So, this method is additionally referred to as the stepping method.
The lengths of horizontal portions are measured and added to induce the full horizontal distance between the points.
The steps might not be uniform, and would depend upon the nature of the earth surface.
Procedure
suppose the horizontal distance between points A and B in Fig. 1.10 is to be measured.
The line AB is first ranged properly. Then, the follower holds the zero end of the tape at A.
The leader selects a suitable length API so that PI is at chest height and API is just horizontal. The horizontality is maintained by eye estimation, by tri-square or by wooden set-square.
The point P2 is marked on the ground by plumb-bob so that P1 is just over P2. The horizontal length AP1 is noted.
Then the follower moves to the position and holds the zero end of the tape at that point.
Again the leader selects a suitable length P2P3 in such a way that P2P3 is horizontal and P4P5 vertical. Then the horizontal lengths P2P3 and P4P5 are measured.
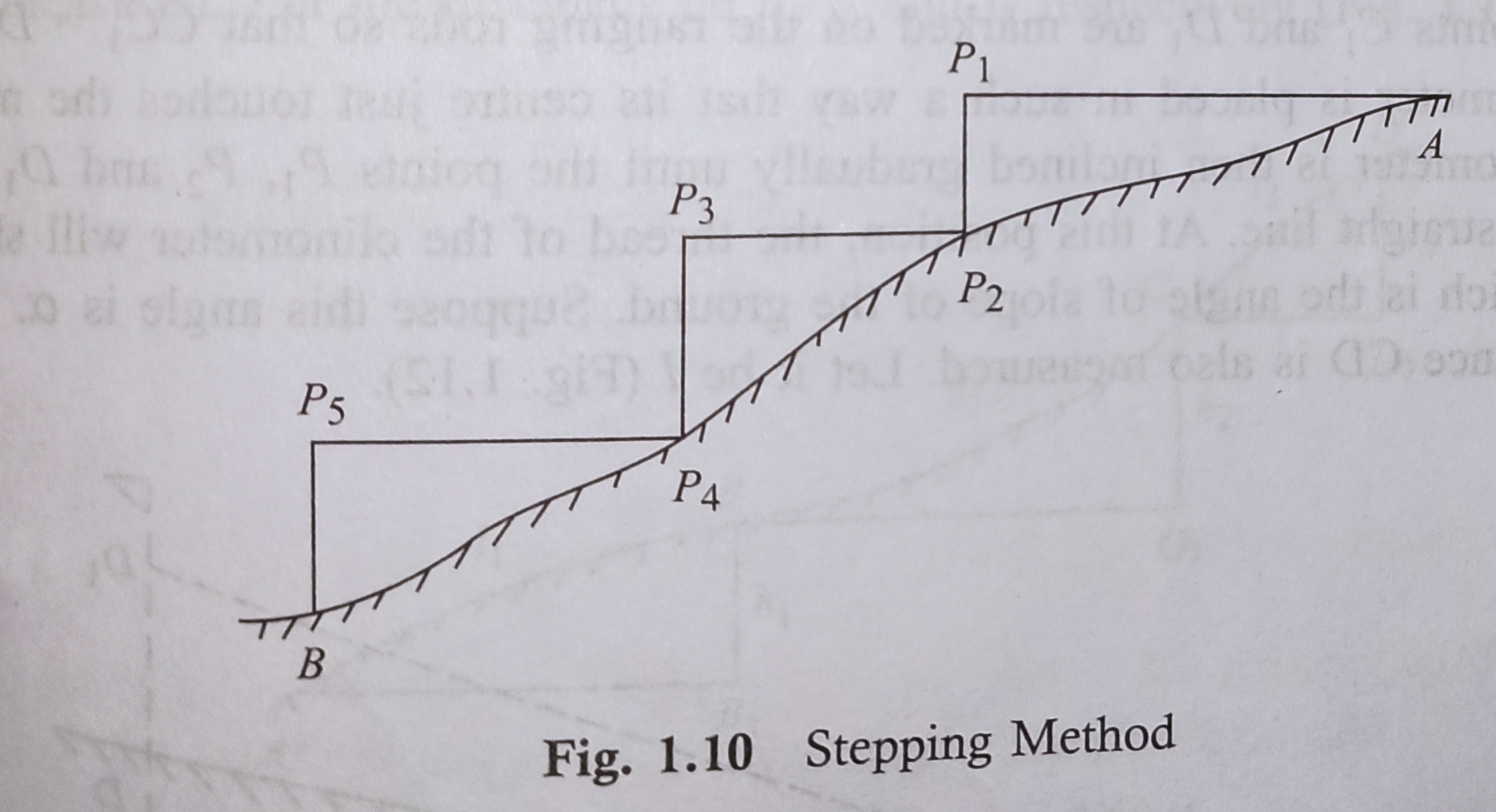
So, the total horizontal length, AB =AP1 + P2P3 + P4P5.
2. Indirect Method
When the slope of the earth surface is long and delicate , the stepping method isn’t suitable. In such a case, the horizontal distance could also be obtained by the subsequent processes:
l. By measuring the slope with a clinometer,
2.By applying hypotenusal allowance, and
3. By knowing the variety of level into the points.
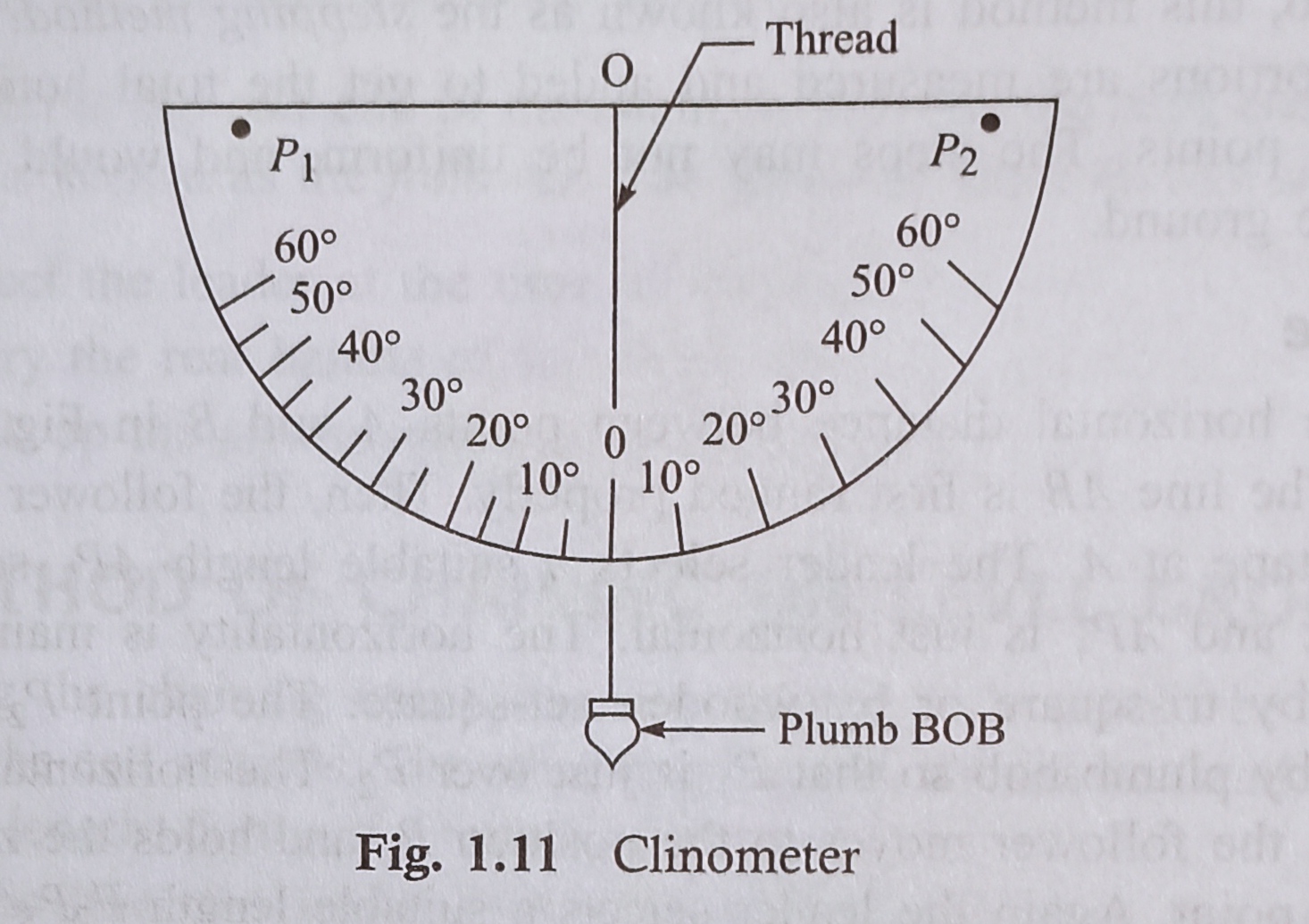
1. Measuring the Slope with a Clinometer
A clinometer may be a graduated semicircular protractor. And it consists of two pins (P1 and P2 in Fig. 1.11) for sighting the thing .
A plumb is suspended from point O with a thread. When the straight edge is simply horizontal, the thread passes through 0°.
When the straight edge is tilted, the thread remains vertical, but passes through a graduation on the arc which shows the angle of slope.
Measurement of Slope and Sloping Distance
Suppose C and D are two points on the sloping ground. Two ranging rods are fixed at these points.
Then 2 several points C1 and D1 are marked on the ranging rods so that CC1 = DD1.
And the clinometer has placed in such a way that its centre just touches the mark Cl.
The clinometer is then inclined gradually until the points P1, P2 and D1 are in the same straight line.
At this position, the thread of the clinometer will show an angle which is the angle of slope of the ground. Suppose this angle is α .
The sloping distance CD is also measured. Let it be l (Fig.1.12).
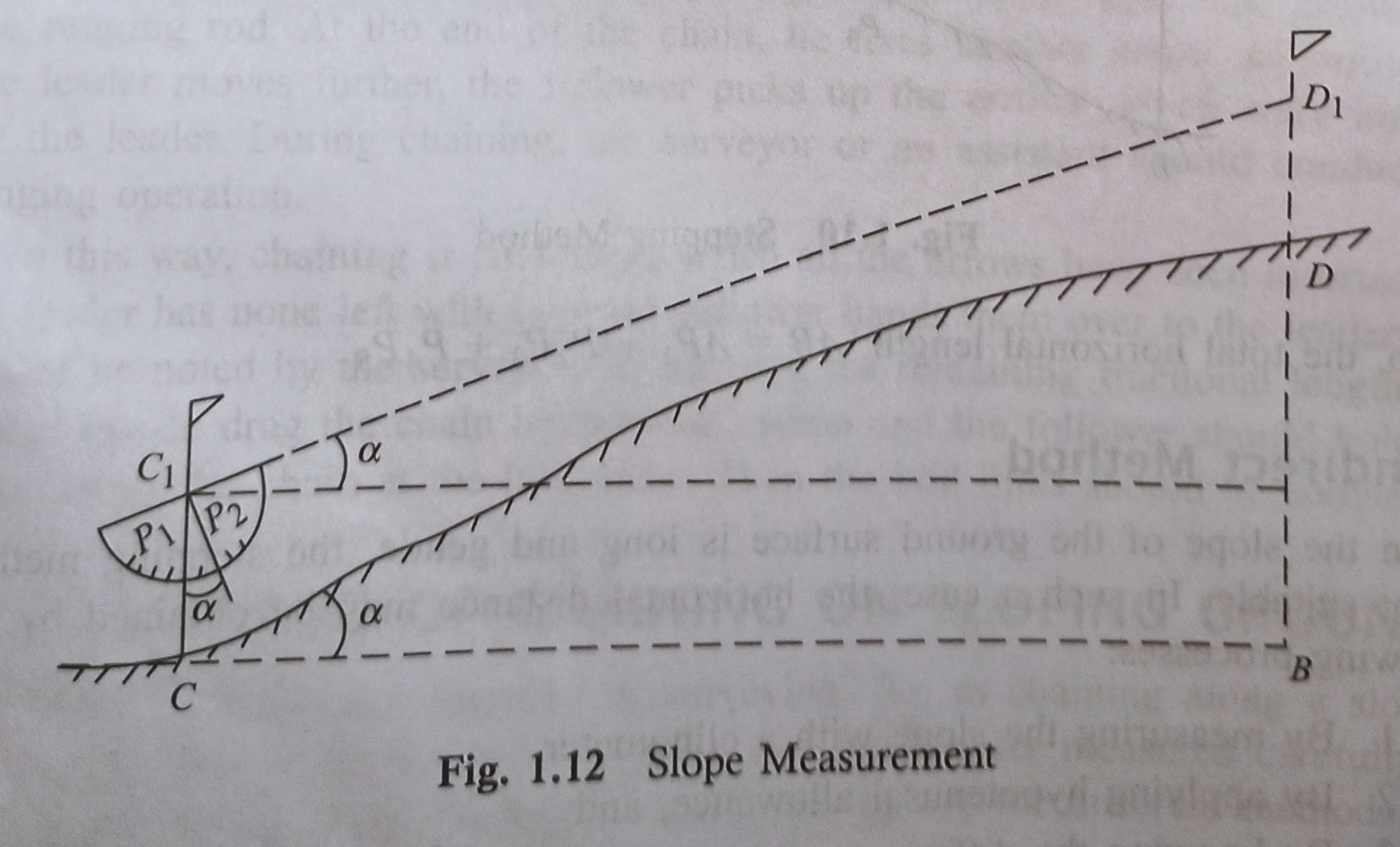
The required horizontal distance, CB = I cosα.
2. Applying Hypotenusal Allowance
Here in this method, the slope of the ground is first found out by using the clinometer or
Abney level. Hypotenusal allowance is then made for each tape length (Fig. 1.13).

Let θ= angle of slope measured by clinometer or Abney level
AB=AB1=20 m=100 links
AC=AB secθ = 100 secθ
B1C=AC-AB1=100 secθ – 100 = 100(secθ-1)
The amount 100(secθ-1) is said to be the Hypotenusal Allowance.
When chaining along the slope, one chain can be actually located at BIO But the arrow should be placed at C after making hypotenusal allowance.
The next chain length will start from C. The same principle is followed until the end of the line is reached.
3. Knowing the Difference of Level
Suppose, A, B, C and D are various points on sloping surface of ground. The difference of level between those points has determined by a levelling instrument.
Let the respective differences be h1,h2 and h3. Then the sloping distances AB, BC and CD are measured. Let the distances be l1, l2 and l3 respectively (Fig, 1.14).
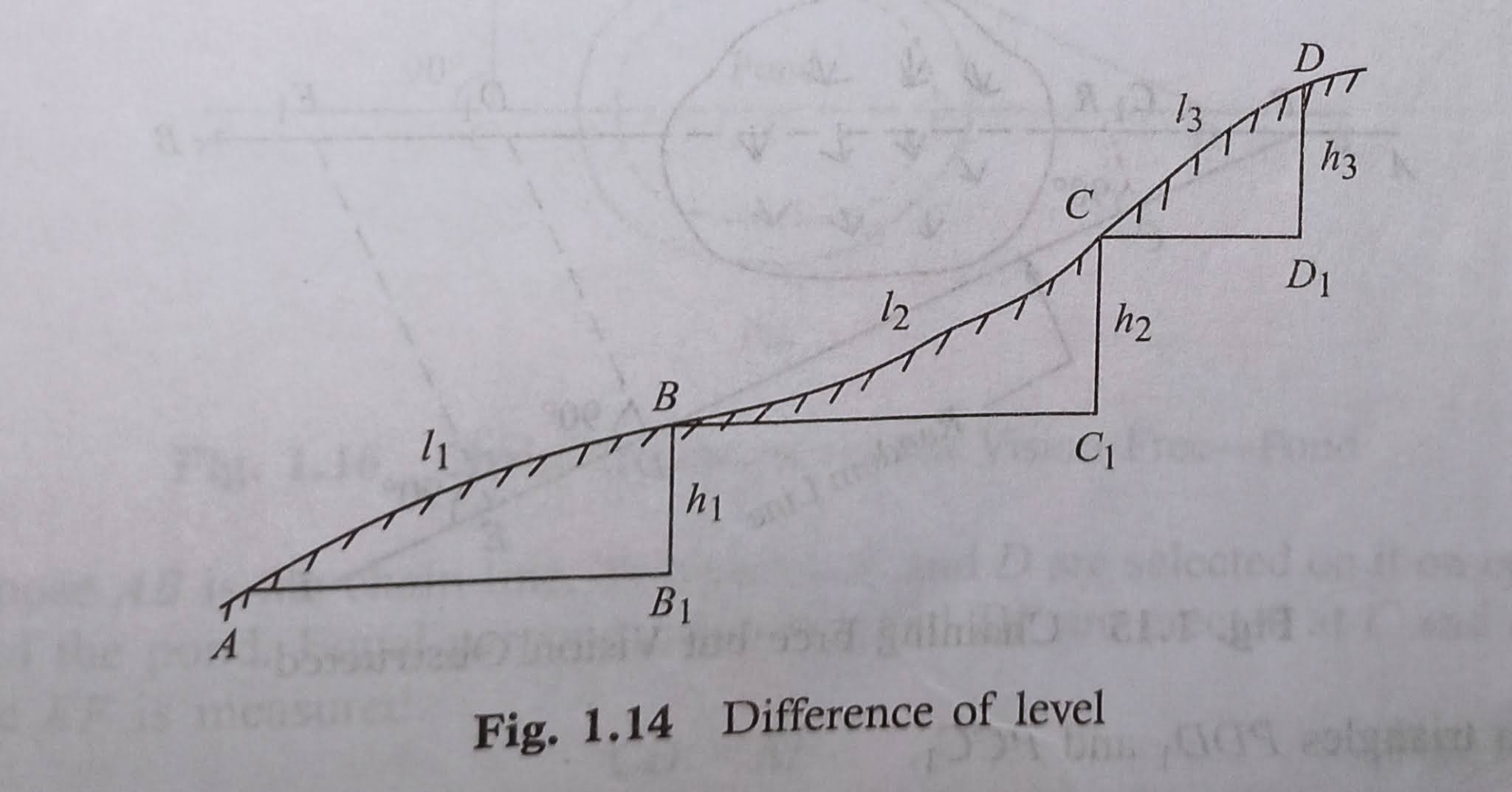
The required horizontal distances are given by
AB1=√(l1^2-h1^2) BC1=√(l2^2-h2^2) CD1=√(l3^2-h3^2)
Total horizontal distance= AB1+BC2+CD1.
Obstacle In Chaining
A chain line could also be interrupted within the following situations:
l. When the chaining is free, but vision is obstructed,
2. When the chaining is obstructed, but vision is free, and
3. When the chaining and vision are both obstructed.
1. Chaining Free but Vision Obstructed
Such a tangle arises when a rising ground or a jungle area interrupts the chain line. Here, the top stations aren’t intervisible. There could also be two cases.
✓ Case I the top stations could also be visible from some intermediate points on the rising ground. during this case, reciprocal ranging is resorted to, and also the chaining is completed by the stepping method.
✓ Case II the top stations aren’t visible from intermediate points when a jungle area comes across the chain line. during this case the obstacle could also be crossed over employing a random line as explained below:
Let AB be the particular chain line which can’t be ranged and extended due to interruption by a jungle.
Supposed, the chain line be extended up to R. a point P is chosen on the chain line and a random line PT is taken during a suitable direction.
And points C, D and E are selected on the random line, and perpendiculars are projected from them. The normal at C meets the chain line at C1.
Theoretically, the normal at D and E will meet the chain line at D1 and E1.
Then, the distances PC, PD, PE and CC1 are measured (Fig. 1.15).
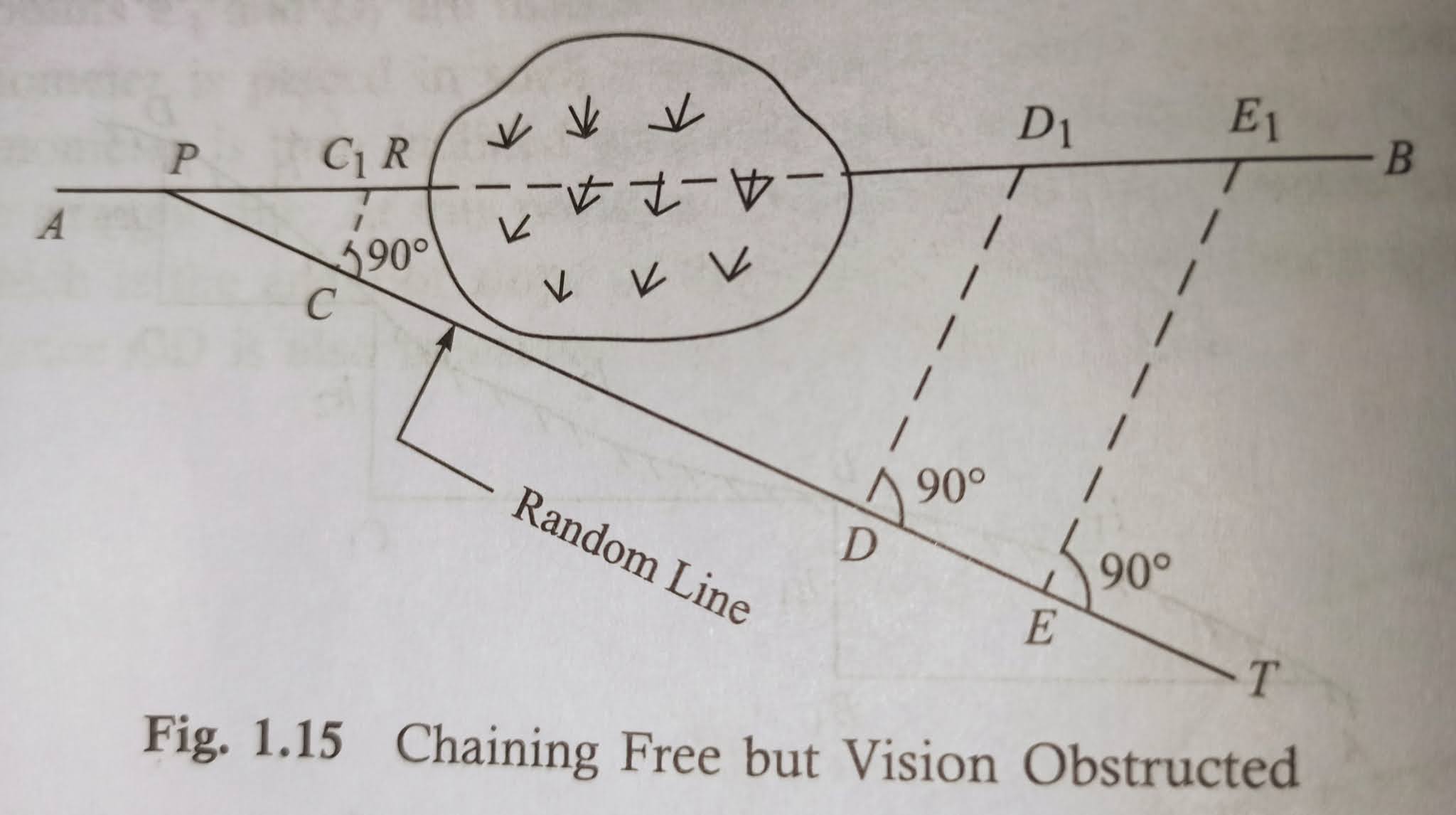
From triangles ∆PDD1 and ∆PCC1,
DD1/PD=CC1/PC
DD1=CC1×PD/PC …………(1)
Again from the triangle ∆PEE1 and ∆PCC1,
EE1/PE=CC1/PC
EE1=CC1×PE/PC………….(2)
From equations (1) and (2), the lengths DD1 and EE1 are calculated.
Here these calculated distances are measured along the normal at D and E. Points D1 and E1 should lie in the chain line AB, that can be extended accordingly
Distance PE1=√(PE^2+EE1^2).
2. Chaining Obstructed but Vision Free
Such a problem arises while a pond or a river comes across the chain line. The situations would be tackled in the following ways.
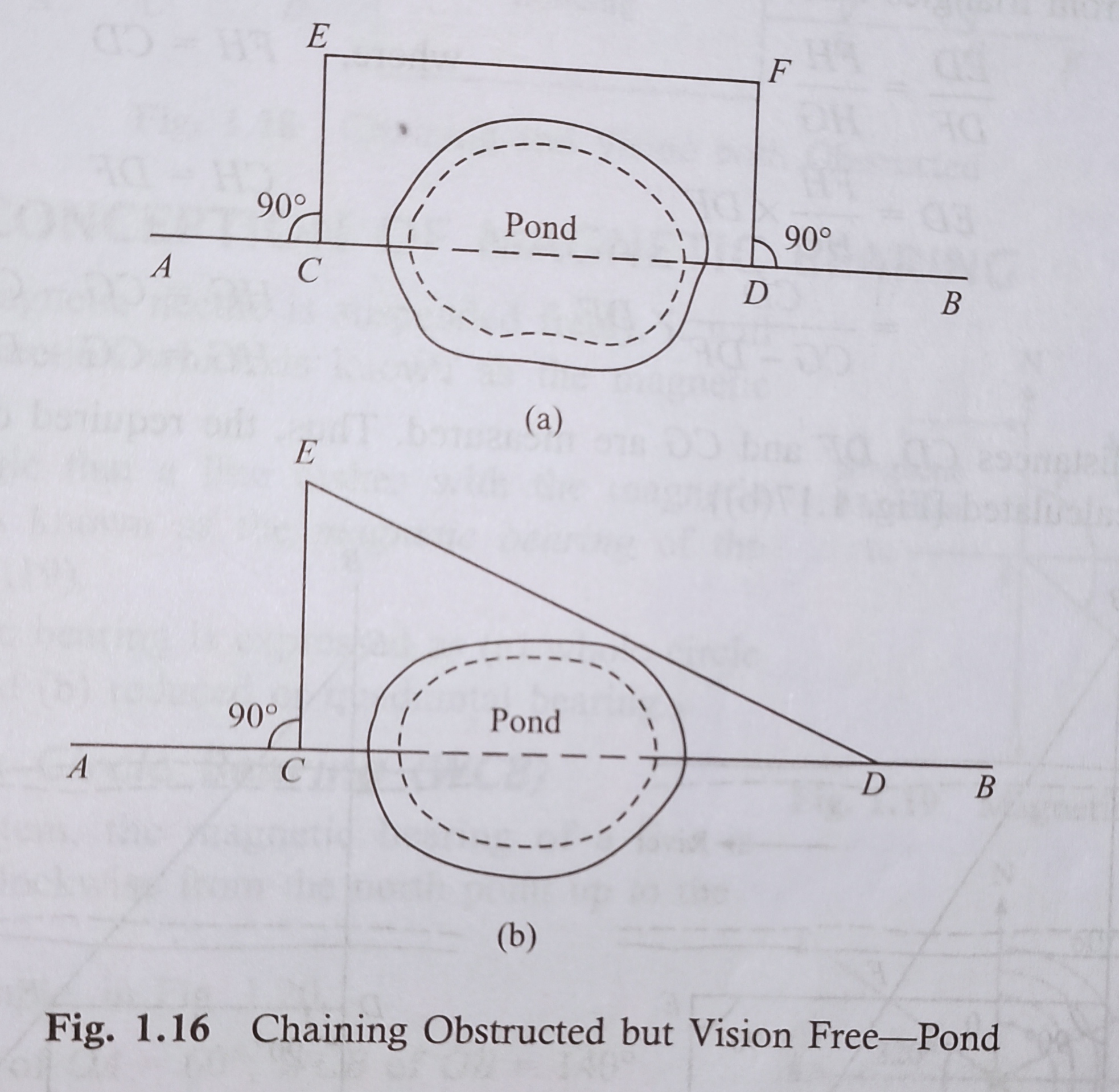
✓ Case I While a pond interrupts the chain line, it is possible to go around the obstruction.
Let AB is the chain line. Two points C and D are selected on it on opposed banks of the pond. Equal normals CE and DF are erected at C and D. The distance EF is measured.
Here, CD=EF. Fig. 1.16(a)
The pond will also be crossed by forming a triangle as shown in Fig. 1.16(b). A point C is selected on the chain line.
The normal CE is set out at C, and a line ED has suitably taken. The distances CE and ED are measured.
So,
CD=√(ED^2 -CE^2)
✓Case II Sometimes it’s not possible to go around the obstruction.
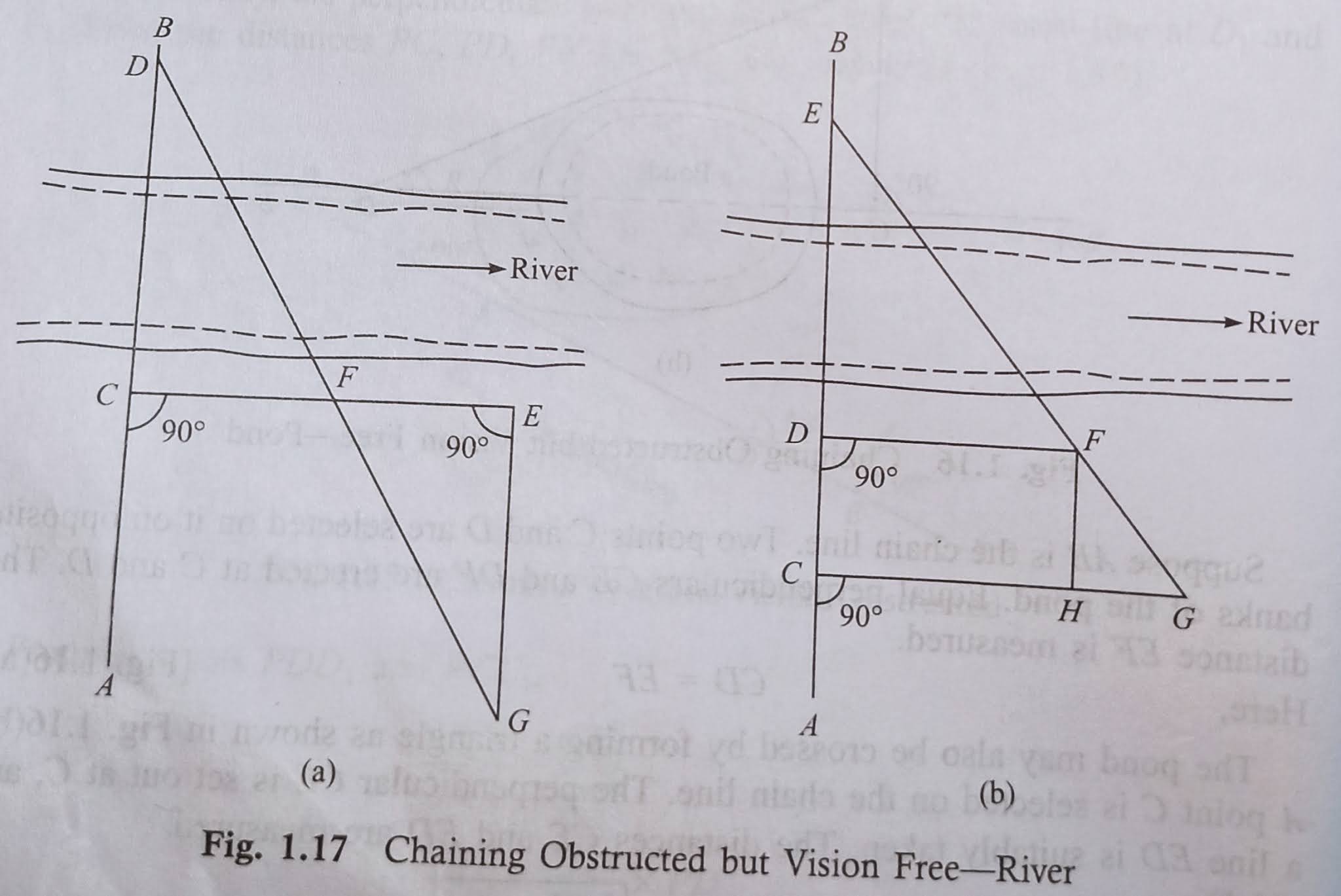
(a) Ideate a small river comes across the chain line. Let AB is the chain line. Two points C and D are selected on this line on opposite banks of the river.
At C, a perpendicular CE is erected and bisected at F. A perpendicular is set out at E and a point G is so selected on it that D, F and G are in the same straight line.
From triangles DCF and GEF,
GE=CD
Then the distance GE has measured, and thus the distance CD is obtained indirectly [Fig. 1.17(a)].
(b) Consider the case when a large river interrupts the chain line.
Let AB be the chain line. Points C, D and E are selected on this line such that D and E are on opposite banks of the river.
The perpendiculars DF and CG are erected on the chain line in such a way that E, F and G are on the same straight line. The line FH is taken parallel to CD.
Now, from triangles DEF and HFG,
ED/FH=FH/HG where,FH=CD
ED=FH×DF/HG CH=DF
=CD×DF/(CG-DF). HG=CG-CH,
Therefore HG=CG-DF
The distances CD, DF and CG are measured. Thus, the required distance ED can be calculated [Fig. 1.17(b)].
3. Chaining and Vision both Obstructed
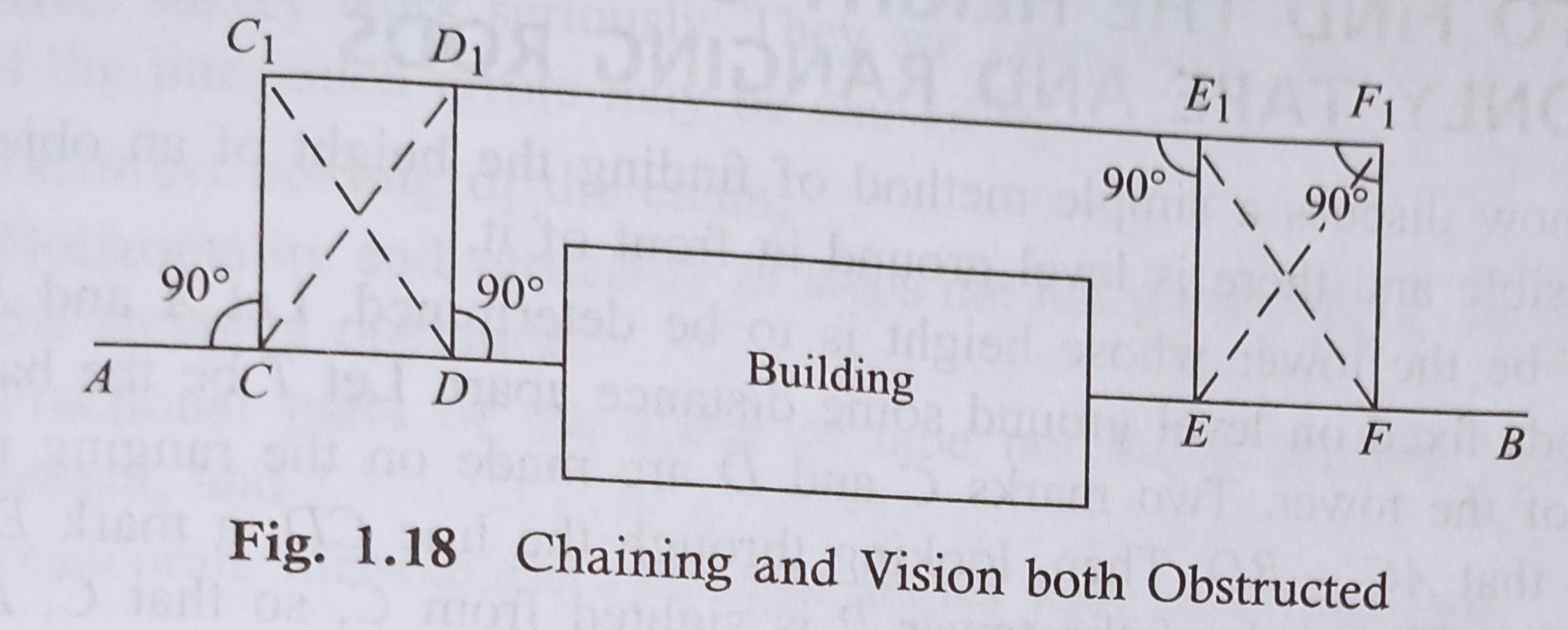
Certain a problem arises while a building comes across the chain line. it’s solved within the following manner.
Suppose AB is that the chain line. Two points C and D are selected thereon at one side Of the building. Equal perpendiculars CC1 and DD1 are erected. the line C1D1 is extended until the building is crossed.
Here on the expanded line, two points E1 and F1 are selected. Then the normals E1E and F1F are so erected that E1E=F1F= D1D=C1C
Thus, the points C, D, E and F will lie on an equivalent line AB.
Here, DE=D1E1
The distance D1E1 is measured, and is capable the specified distance DE (Fig. 1 . 1
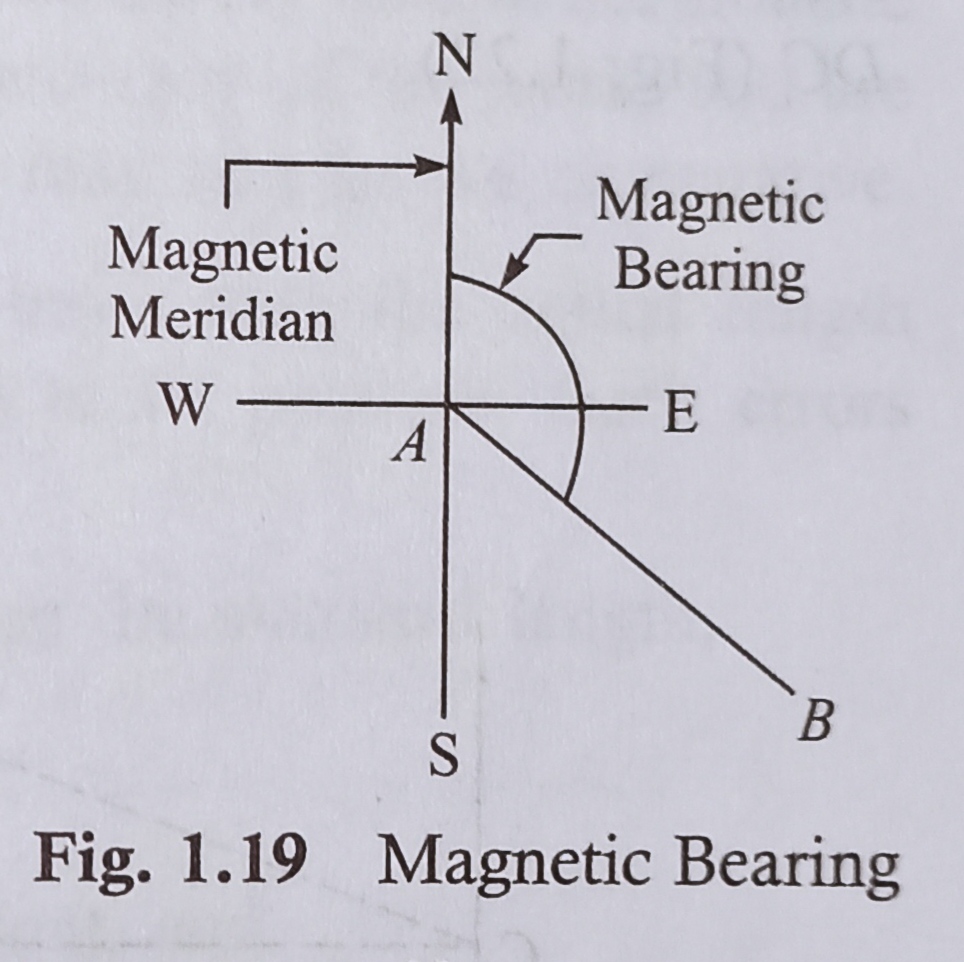
Conception Of Magnetic Bearing
When a magnetic needle is suspended freely, it wil show a direction which is known as the magneti meridian.
The angle that a line makes with the magneti maridian is known as the magnetic bearing of th line (Fig. 1.19).
Magnetic bearing is figured as
(a) whole circle bearing, and
(b) reduced or quadrantal bearing.
Whole Circle Bearing (WCB)
In this system, the magnetic bearing of a line is measured clockwise from the north point up to the line.
For example, in Fig. 1.20,
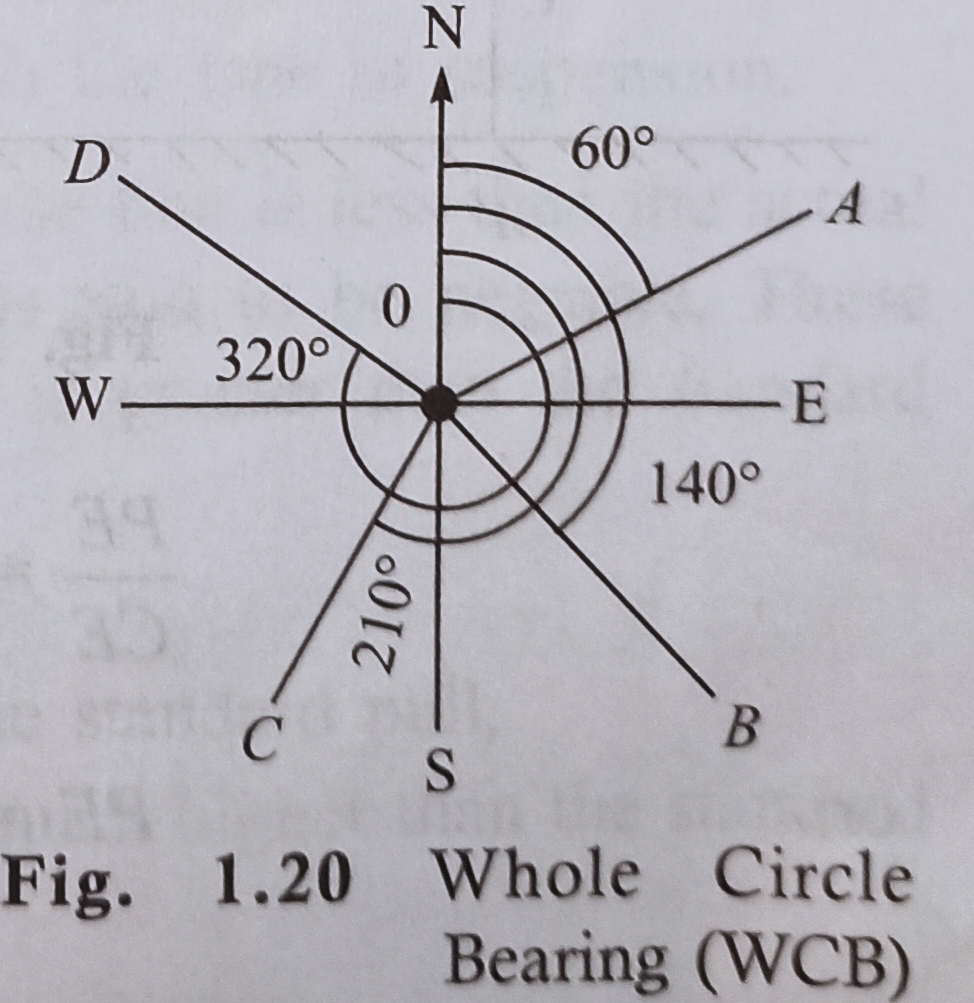
WCB of OA=60°; WCB of OB=140°
WCB of OC=210°; wCB of OD=320°
Reduced Bearing (RB)
In this system, bearing is measured clockwise or anticlockwise from the north or south towards the east or west.
Hence, four quadrants are considered and are denoted as NE, NW, SE and SW. The values of RB may lie between 0° and 90°, but the quadrants might be mentioned too (Fig. 1.21).
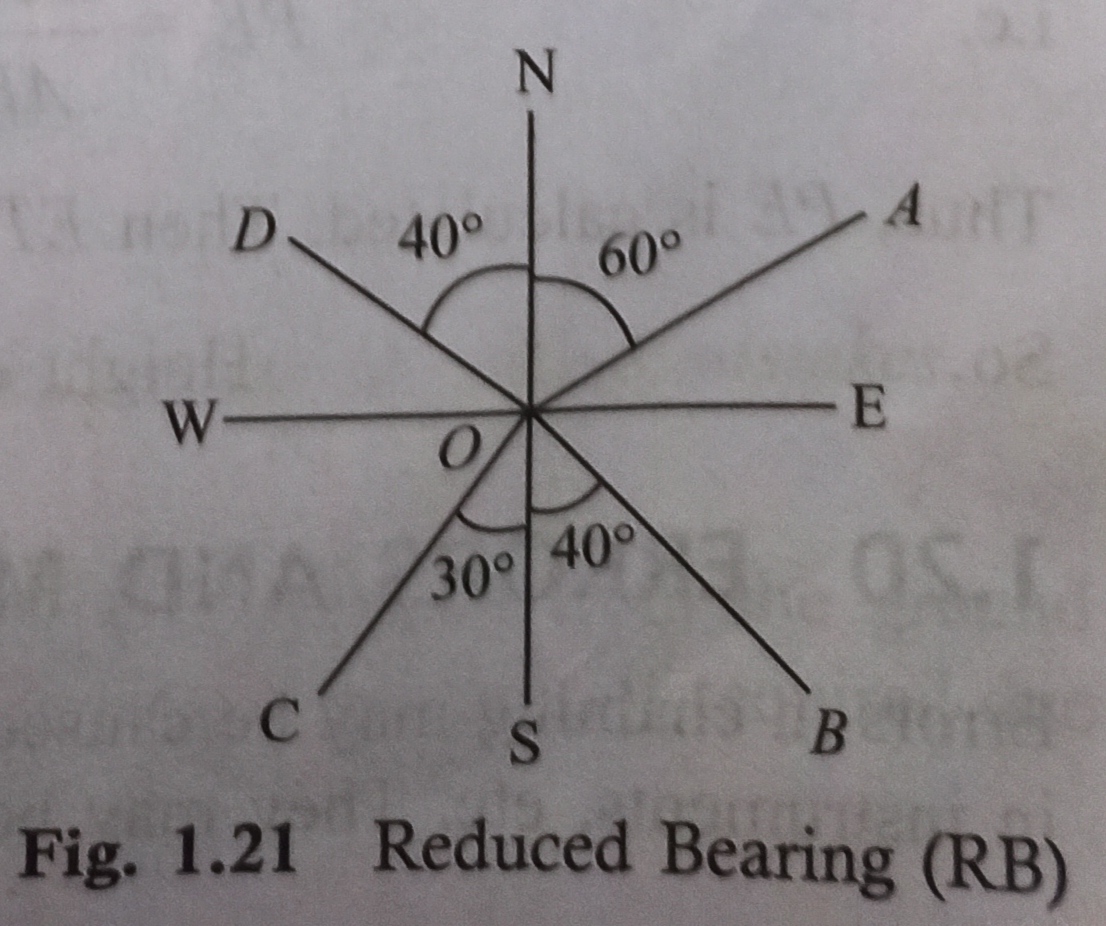
For example, in Fig. 1.21,
RB of OA=N60°E
RB of OB=S40°E
RB of OC=S30°W
RB of OD=N40°W
About Post
Here in this post we covered the Method of Chaining on level ground and slope ground , obstacle in chaining and conception of magnetic bearing.

